

Quantization of the gravitational field is a major fundamental open problem of modern theoretical physics. One of the general research frameworks aiming to understand the structure of quantum gravity (QG) is the covariant Loop Quantum Gravity approach, and for the past 30 years there has been substantial progress regarding the construction of mathematically rigorous definitions of QG, called spinfoam models. While successful in describing gravity, these models generally fail to describe matter fields, due to the specific structure of the relevant gauge symmetry group. The aim of our Project is to construct a novel, more general QG model, which includes matter fields. Our method is based on the generalization of the notion of a symmetry group using category theory, specifically a mathematical framework called Higher Gauge Theory. This generalization allows us to treat gravity, gauge fields, fermions, and scalars on equal footing, using the algebraic structure called a 3-group, and perform the spinfoam quantization program for all fields simultaneously. Therefore, the expected result is a well-defined spinfoam-like QG model, which describes not just gravity, but all matter fields as well. Such a model would represent a major improvement over existing state-of-the-art spinfoam models. Its main impact would be to open up a new field of study which nontrivially involves matter in a QG context, enabling us to rigorously study a lot of scenarios that were previously out of our reach. In particular, this would potentially provide novel ways to address longstanding open questions such as the resolution of cosmological and black hole singularities. Another impact could be further development of the Higher Gauge Theory approach as a coherent framework to investigate more speculative questions of Standard Model physics, such as the origin of particle families, the origin of coupling constants and free parameters, physics at and beyond grand-unified scales, and so on.

Formulation of the quantum theory of the gravitational interaction is one of the main outstanding problems of modern theoretical physics. Our current knowledge of fundamental physics rests on two well-founded theories --- the Standard Model (SM) of elementary particles, and the theory of General Relativity (GR). The former provides a precise quantum description of all known fields in Nature, except gravity. The latter provides a precise classical description of gravity, and is thus incompatible with the quantum theory. The quantization of gravity, and the unified description of both gravitational and matter fields within a single theoretical framework, has often been poetically called the holy grail of modern theoretical physics, and its theoretical significance and importance cannot be overstated.
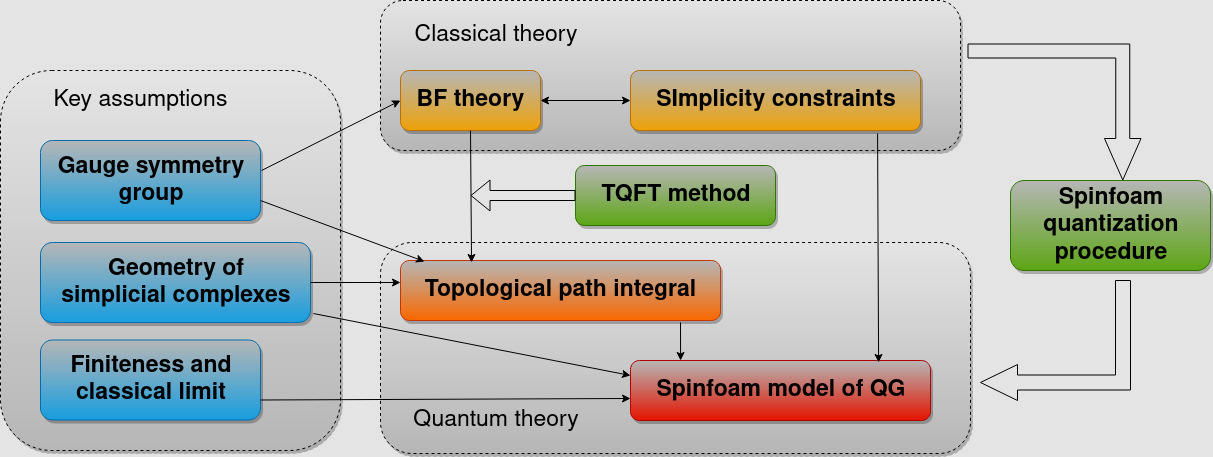
Since the inception of quantum theory and general relativity at the beginning of the XX century, there has been a strong incentive in the fundamental theoretical physics community towards the goal of constructing a quantum theory of gravity. A whole plethora of research directions has been developed over the years, maturing into vast research frameworks such as String Theory, Loop Quantum Gravity (LQG), Noncommutative Geometry, Causal Set Theory, and many others. Within the LQG framework [1,2], one promising research direction has emerged in the past 30 years, focused on the construction of explicit mathematical models of QG called spinfoam models [3]. The core idea is to perform the so-called spinfoam quantization procedure, with the goal of obtaining a precise and rigorous definition of the gravitational path integral. The procedure consists of three fundamental steps:
The method rests on several key assumptions. In step (1), the key assumption is a wise choice of the variables and form of the classical action, guided by the appropriate group of gauge symmetries. In step (2), the key assumption is a piecewise-flat description of the spacetime manifold (a simplicial complex), using the mathematical tools of algebraic topology and group representation theory within the TQFT framework. In step (3), the key assumption is a set of physical requirements: that the resulting quantum theory has a correct classical limit, that it must be finite (both UV and IR complete), and that it has otherwise acceptable and desired physical features (such as a potential to resolve cosmological and black hole singularities). The diagram below illustrates the spinfoam quantization procedure.
Historically, the first spinfoam model was the Ponzano-Regge model [4] for 3D gravity, formulated in 1968. Since then, various models have been constructed in various spacetime dimensions [6,7,8], each model being more sophisticated than previous models in its features and better in satisfying the above physical requirements. The most sophisticated model so far is the so-called EPRL/FK model [7,8], formulated in 2008. It was independently obtained by two research groups, suggesting that this line of investigation of QG is converging toward a single model.
Unfortunately, all spinfoam models share one big drawback --- they all describe pure gravity, without the matter fields present in the Standard Model. While their quantum description of the pure gravitational field is generally considered successful, none of the models can include gauge bosons, fermions, and scalars in a unified description of gravity and matter, despite various attempts to incorporate matter into the existing spinfoam models (see for example [8]). Without matter, one cannot employ these models to study arguably the most interesting aspects of QG, including resolutions of cosmological and black hole singularities.
The main goal of the QGHG-2021 project is to generalize the construction of spinfoam models in a way that includes matter fields together with gravity in a unified spinfoam-like QG model. Such a model can then be studied and applied to problems that involve matter coupled to gravity, which are beyond the scope of existing spinfoam models.
The analysis of the reasons why matter is so hard to include into spinfoam models points to the properties of the Lie group as a mathematical structure that encodes the gauge symmetry of the model (the Lorentz group, SO(3,1), in particular). As it turns out, a Lie group appears to be an inadequate algebraic structure for the description of the gauge symmetry, and there exists a more general algebraic structure that is more appropriate for the spinfoam quantization procedure [9].
Namely, the concept of a group can be generalized using the abstract methods of higher category theory, to obtain so-called higher gauge structures, such as a 2-group, a 3-group, and so on. A framework called Higher Gauge Theory (HGT) has been recently introduced [10] to encompass the mathematical formalism which generalizes the notions such as the connection, parallel transport along a curve, and holonomy, to higher dimensions: an n-connection, parallel transport along an n-dimensional manifold, and n-holonomy. The central algebraic structure which establishes this generalization is the notion of an n-group: an n-category with only one object and invertible morphisms, 2-morphisms, and up to n-morphisms. As a synergy of higher category theory and algebraic topology, HGT is today a very active research area of mathematics, with novel applications to TQFT.
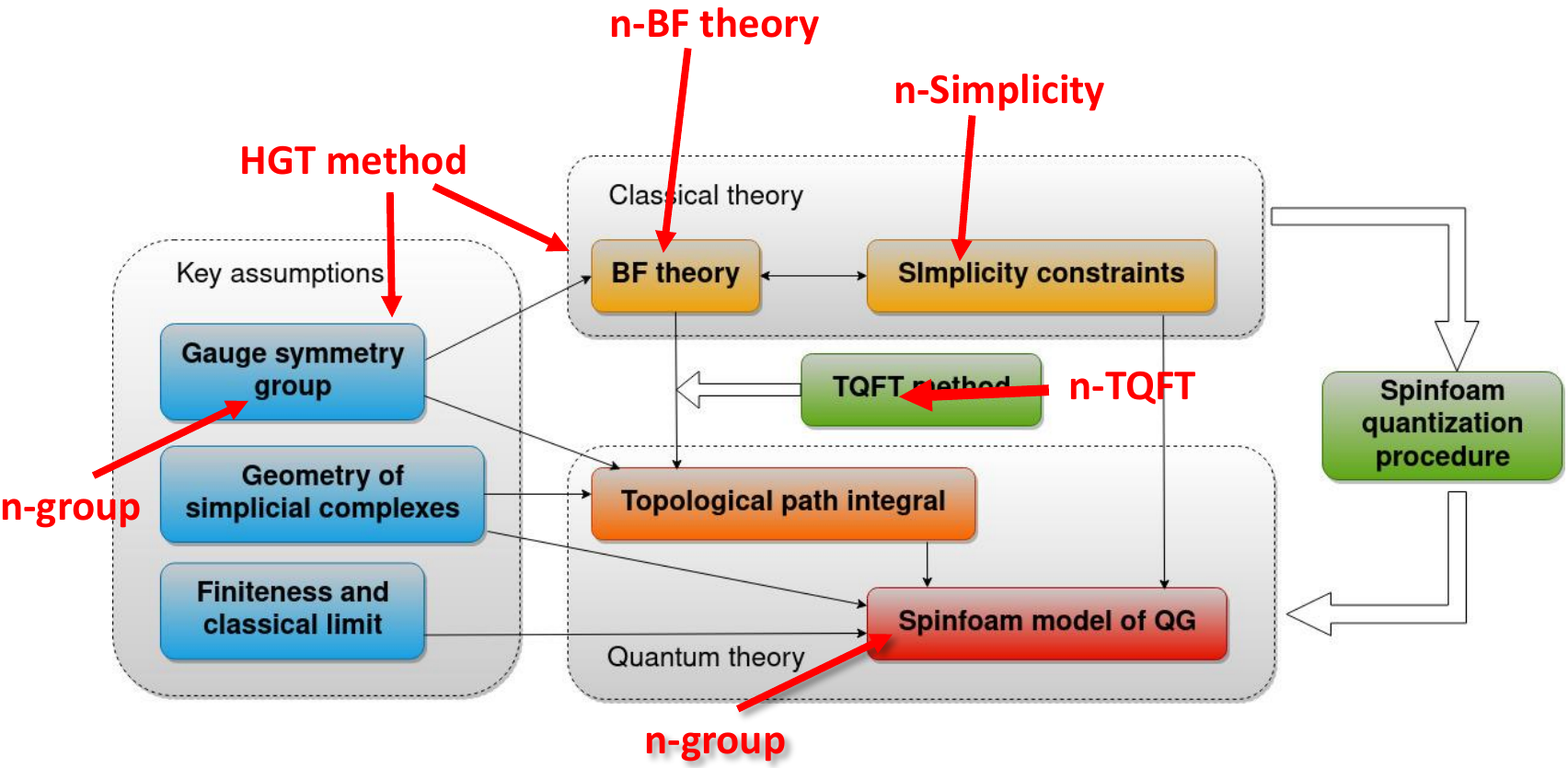
The application of HGT to theoretical physics is centered on the use of n-groups to describe the concept of gauge symmetry, instead of using Lie groups. The diagram below illustrates its influence in the spinfoam quantization procedure, indicated with red arrows.
Recently, the notion of a 2-group has been successfully employed to construct a generalization of spinfoam models, called a spincube model [9,11,12]. The main insight is that the 2-group structure naturally incorporates the tetrad fields in the topological sector of the classical action (called 2BF action [13]), in contrast to the traditional Plebanski action [14] which is used as a starting point for the construction of existing spinfoam models. The presence of tetrad fields in the topological sector allows one to quantize them in step (2) of the spinfoam quantization procedure, which in turn opens up a possibility to add matter fields to the QG model in a straightforward way. Various groups of researchers have studied related 2-group structures, with the aim of performing the step (2) rigorously, mostly for models in Euclidean spacetime [15,16,17]. On the math side, a representation theory of 2-groups has been developed [18], generalizing the representation theory of ordinary Lie groups, in the context of HGT.
Finally, in 2019. we have generalized the model even further, using the 3-group [19] as a fundamental algebraic structure [20]. Based on a triple of Lie groups, (G, H, L), a 3-group turns out to be an excellent structure to describe not just gravity, but matter fields as well. Just as the gauge group SU(3)xSU(2)xU(1) gives an algebraic classification of gauge fields in the Standard Model, the 3-group gives an algebraic classification of the entire spectrum of fields --- gravity (Lie group H), gauge bosons (Lie group G), and most importantly, fermions and scalars (Lie group L). This structure was our main insight in [20], and we have successfully performed the step (1) of the spinfoam quantization procedure, constructing a constrained 3BF action which features the whole Standard Model coupled to Einstein-Cartan gravity as a classical theory. This result has paved the way for the possibility of performing steps (2) and (3) of the spinfoam quantization procedure, and formulating a QG model that features both matter and gravity on equal footing. The aim of the QGHG-2021 project is to complete the spinfoam quantization procedure initiated in [20], and thereby arrive at a specific QG model which incorporates all known fields in a unified way.
Moreover, the presence of the Lie group L, within the 3-group structure, opens up novel and intriguing avenues of research. Specifically, the group L is responsible for the description of fermionic and scalar fields, and dictates the number and properties of the matter fields present in the theory. The choice of the group L therefore contains information about particle families, baryon and lepton numbers, and other symmetries of the matter sector of the SM. It is thus quite interesting to study various 3-groups in this context, since there may exist a choice of the group L which gives a natural explanation for the symmetries of matter fields. Combined with the symmetries of the gauge boson sector (group G) and gravity (group H), the whole 3-group could go beyond the SM description, by offering a nontrivial algebraic description of all presently known fields in Nature.
As a final comment on methodology, we ought to make a remark regarding the actual usefulness of both spinfoam models and their proposed generalizations. While the construction of a QG model is by far the most important problem, the resulting mathematical formulation of the model often ends up being quite complicated. This means that the analytical solutions of the model are hard to come by, and the only way to effectively study the properties of the model is via numerical methods. The software which supports such numerical calculations exists only for certain special cases, notably for the Causal Dynamical Triangulations research direction [21]. To be able to efficiently study the properties of a more general class of QG models, including the one we aim to construct, it is important to develop a software library of mathematical algorithms optimized for numerical calculations involving 4-dimensional simplicial complexes of pseudo-Riemannian manifolds. We believe that it is best to develop such software in parallel with the development of the QG model itself. Thus, a second goal of the QGHG-2021 project is to provide the groundwork for such a software library, with a long-term goal of using it to numerically study various aspects of the behavior of the proposed QG model, such as the resolution of cosmological and black hole singularities.
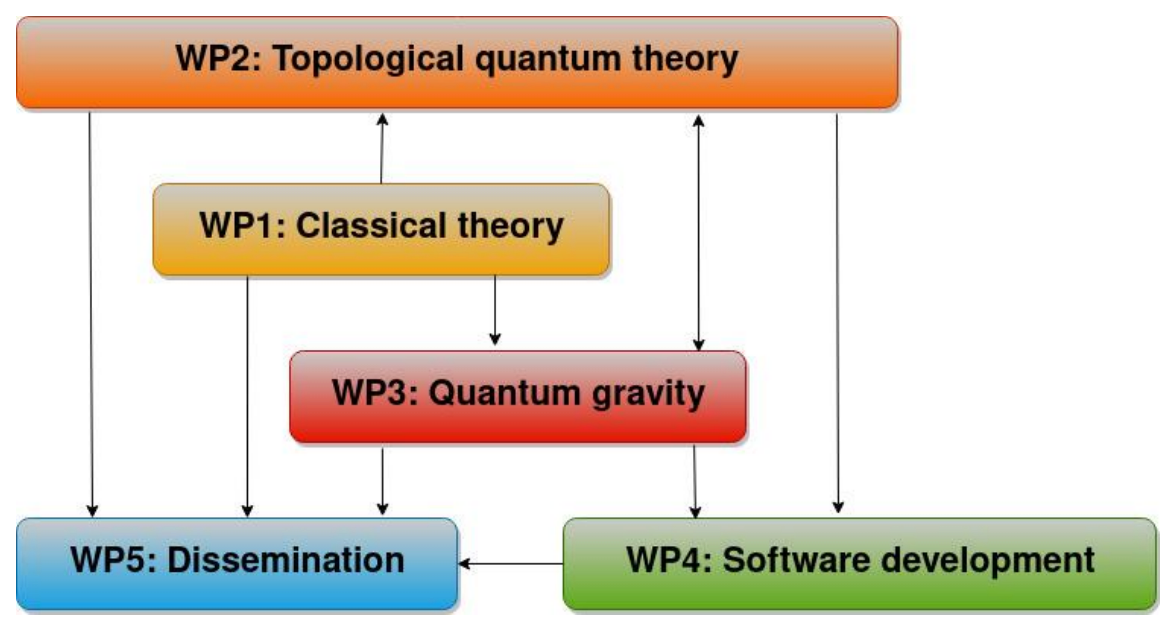
The work plan can be outlined as follows:
These topics are organized in so-called work packages, and they inform each other as indicated on the following diagram:
The central aim of the QGHG-2021 project is to apply the spinfoam quantization procedure (expressed in the three main steps in the Introduction above) to the theory of gravity coupled to matter fields, using the algebraic structure of a 3-group to describe the gauge symmetry, and exploiting the underlying mathematical framework of HGT. The goal is to construct a viable model of QG with matter fields, based on the classical theory and relevant 3-group structure developed in [20]. The planned tasks are concrete steps one should take to appropriately generalize and implement the spinfoam quantization procedure.
The second objective of the project is to develop a software library for numerical investigation of QG models based on state sums and simplicial complexes. The development of the software will be done in collaboration with a professional software engineer as a subcontractor of the project.
Finally, throughout the duration of the project, we will aim to disseminate the results of our research, and to engage in active collaboration with several research groups abroad, including members from both physics and mathematics. We will also engage in public outreach, leveraging the public interest in fundamental science to promote open-mindedness and critical thinking to the general public.
[1] C. Rovelli, Quantum Gravity, Cambridge University Press, Cambridge (2004).
[2] T. Thiemann, Modern Canonical Quantum General Relativity, Cambridge University Press, Cambridge (2007).
[3] C. Rovelli and F. Vidotto, Covariant Loop Quantum Gravity, Cambridge University Press, Cambridge (2014).
[4] G. Ponzano and T. Regge, "Semiclassical limit of Racah coefficients", in "Spectroscopic and Group Theoretical Methods in Physics" ed. F. Bloch, North Holland Publishing, Amsterdam (1968).
[5] J. W. Barrett and L. Crane, J. Math. Phys 39, 3296 (1998), [arXiv:gr-qc/9709028].
J. W. Barrett and L. Crane, Class. Quant. Grav. 17, 3101 (2000), [arXiv:gr-qc/9904025].
H. Ooguri, Mod. Phys. Lett. A 7, 279 (1992), [arXiv:hep-th/9205090].
[6] J. Engle, E. R. Livine, R. Pereira and C. Rovelli, Nucl. Phys. B799, 136 (2008), [arXiv:0711.0146].
[7] L. Freidel and K. Krasnov, Class. Quant. Grav. 25, 125018 (2008), [arXiv:0708.1595].
[8] E. Bianchi, M, Han, E. Magliaro, C. Perini, C. Rovelli and W. Wieland, Class. Quant. Grav. 30, 235023 (2013), [arXiv:1012.4719].
[9] A. Miković and M. Vojinović, Class. Quant. Grav. 29, 165003 (2012), [arXiv:1110.4694].
[10] J. C. Baez and J. Huerta, Gen. Relativ. Gravit. 43, 2335 (2011), [arXiv:1003.4485].
[11] A. Miković, Rev. Math. Phys. 25, 1343008 (2013), [arXiv:1302.5564].
A. Miković, Adv. Theor. Math. Phys. 21, 631 (2017), [arXiv:1402.4672].
[12] M. Vojinović, Phys. Rev. D 94, 024058 (2016), [arXiv:1506.06839].
[13] F. Girelli, H. Pfeiffer and E. M. Popescu, Jour. Math. Phys. 49 032503 (2008), [arXiv:0708.3051].
J. Faria Martins and A. Miković, Adv. Theor. Math. Phys. 15 1059 (2011), [arXiv:1006.0903].
[14] J. F. Plebanski, J. Math. Phys. 18, 2511 (1977).
M. Celada, D. González and M. Montesinos, Class. Quant. Grav. 33, 213001 (2016), [arXiv:1610.02020].
[15] A. Baratin and L. Freidel, J. Math. Phys. 56, 011705 (2015), [arXiv:1409.3526].
[16] A. Baratin and D. K. Wise, AIP Conf. Proc. 1196, 28 (2009), [arXiv:0910.1542].
[17] S. K. Asante, B. Dittrich, F. Girelli, A. Riello and P. Tsimiklis, Class. Quant. Grav. 37, 205001 (2020), [arXiv:1908.05970].
[18] J. C. Baez, A. Baratin, L. Freidel and D. K. Wise, Mem. Amer. Math. Soc. 219, 1032 (2012), [arXiv:0812.4969].
L. Crane and M. D. Sheppeard, [arXiv:math/0306440].
[19] J. F. Martins and R. Picken, Differ. Geom. Appl. Jour. 29, 179 (2011), [arXiv:0907.2566].
W. Wang, Jour. Math. Phys. 55, 043506 (2014), [arXiv:1311.3796].
[20] T. Radenković and M. Vojinović, JHEP 10, 222 (2019), [arXiv:1904.07566].
[21] J. Ambjorn, A. Goerlich, J. Jurkiewicz and R. Loll, Phys. Rep. 519, 127 (2012), [arXiv:1203.3591].